
Knowledge graphs (KGs) are a useful tool for representing rich symbolic knowledge about entities and their relationships, and have been applied in a variety of fields, including search engines, recommendation systems, chatbots, and healthcare. Traditionally, KGs have been constructed through expensive human crowdsourcing efforts (such as WordNet, ConceptNet, and ATOMIC). Researchers have also explored the use of text mining techniques for automatic KG construction, but this remains a challenging task due to large corpus and complex processing required. Besides, an inevitable shortcoming of text mining is that the relations are limited to those covered by the selected corpus. For example, much of the commonsense knowledge would not be explicitly expressed in human languages, making it difficult to extract them from corpus. How to build a knowledge graph of any relations is still an underexplored topic.
There has been a significant increase in the number of deep neural models that have achieved high levels of performance on various tasks across diverse domains, such as language modeling with GPT-3 and ChatGPT, and medical prediction with bioBERT. During the training, these models can store the knowledge learned from data implicitly in their parameters. For instance, a medical model trained on large-scale health records may have acquired a wealth of medical knowledge, allowing it to accurately predict diseases. Similarly, a pandemic prediction model with accurate trend simulation may have implicitly captured certain transmission patterns from the data it was trained on.
Recent research attempted to utilize these LMs as knowledge bases (LAMA). For example, with manually or automatically crafted prompts (e.g., "Obama was born in __") to query the LMs for answers (e.g., "Hawaii") However, the black-box LMs, where knowledge is only implicitly encoded, fall short of the many nice properties of symbolic KGs, such as the ease of browsing the knowledge or even making updates. This leads to the question: can we automatically harvest KGs from the LMs, and hence combine the best of both worlds, namely the flexibility and scalability from the neural LMs, and the access, editability, and explainability in the symbolic form?
This work represents a step towards achieving this goal. Our automatic framework is able to efficiently and scalably extract a knowledge graph (KG) from a pretrained language model (LM) such as BERT or RoBerta, resulting in a family of new KGs (e.g., BertNet, RoBertaNet) that provide a broader and extendable set of relations and entities beyond those in existing hand-annotated KGs like ConceptNet.
In the following, we’ll briefly present our framework. Please refer to our paper for more details. We have released our code and the outcome KGs from on Github, and you are also welcome to try out our knowledge server demo! (Figure 1)
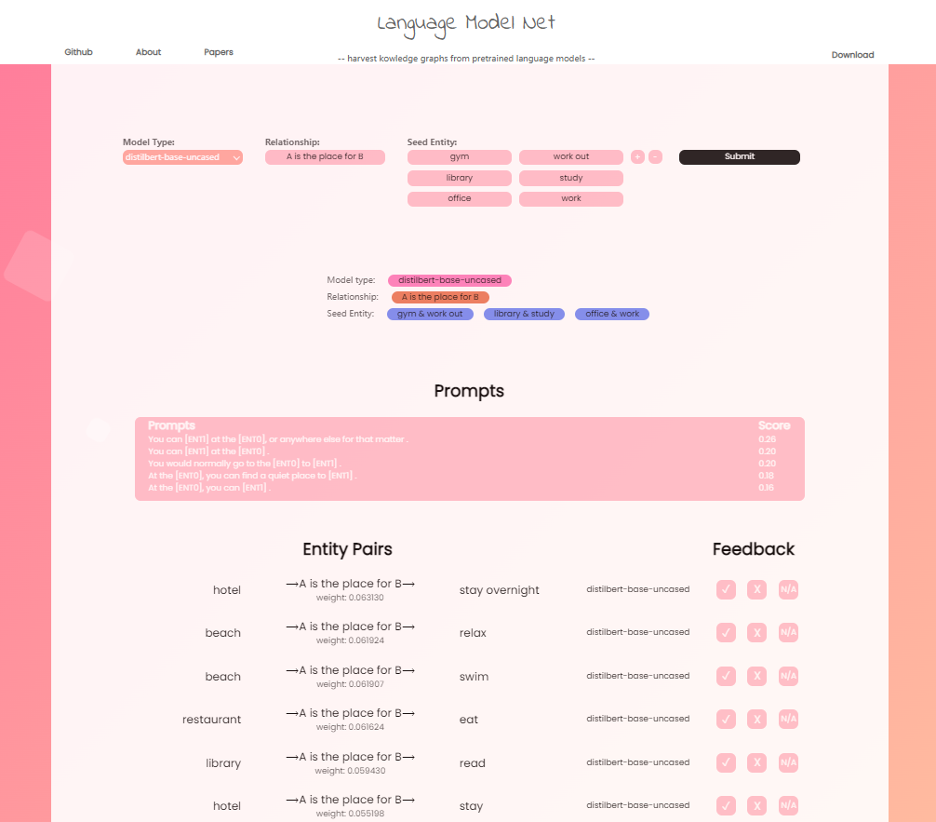
Our framework to harvest KGs from LMs
We first formulate the problem: given a description of a relation, we want to harvest entity tuples of this relation from a language model. Here, a relation is framed as a prompt with entity slots which is further disambiguated with a handful of example seed entity tuples. With these inputs, our framework is expected to output a list of entity tuples with confidence (Figure 2).
Compatibility Score
Before we dive into the two main stages of our framework, we introduce the compatibility score between a prompt and an entity tuple.
\[ f_{L M}(\langle h, t\rangle, p)=\\\alpha \log P_{L M}(h, t \mid p)+(1-\alpha) \min \left\{\log P_{L M}(h \mid p), \log P_{L M}(t \mid p, h)\right\} \]
With BERT as an example, the first term in the scoring function involves the probability of filling the entity tuple $<h, t>$ into the slots in the prompt $p$. Typically, this joint probability of entity pairs can be decomposed to $P_{LM}(h|p) \times P_{LM}(t|h,p)$, assuming it’s computed in an autoregressive style. Besides, we also want to make sure that the probability of each step shouldn’t be too low, and that’s the intuition behind the second term. A concrete example is shown in Figure 1, where p=“A is the place for B”, h=“library” and t=“study”. We also present how to process multi-token entities where h=“study room”.
With this compatibility score, we then introduce the workflow of harvesting knowledge graphs from language models (Figure 2), which can be divided into two main stages: Prompt Creation and Entity Tuple Search.
Stage 1: Prompt Creation
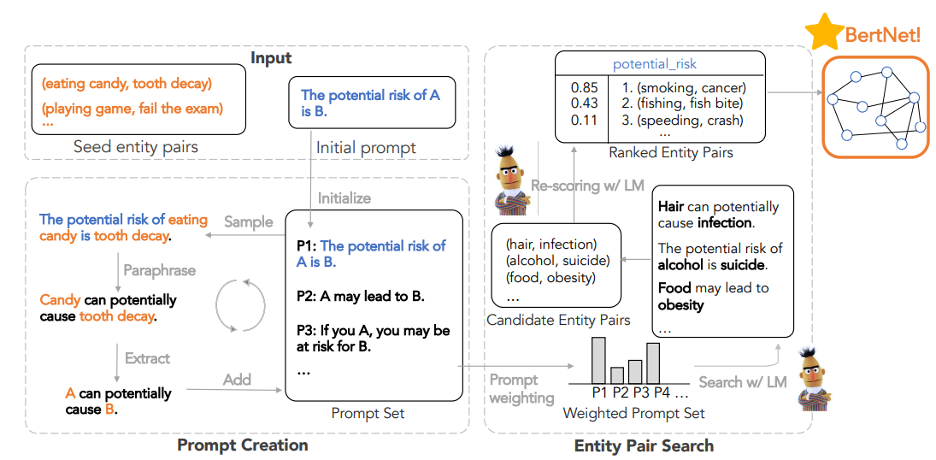
A known deficiency of language models is their inconsistency when given different prompts. Sometimes even a slight difference in wording would cause a drastic change in the prediction results. To this end, we want to generate multiple paraphrases of the initial input prompt, and use them to regularize the output of language models.
As our implementation, the algorithm iteratively samples entity tuples and prompts to assemble a statement and paraphrase it (specifically, usingGPT-3 API). The process is shown in the left part of Figure 2. The generated prompts can be semantically drifted, so the prompts are weighted by the average compatibility scores between a prompt and all given seed entity tuples. The weights are further normalized with softmax across all prompts. The resulting weighted prompt set serves as a more reliable description of the relation.
Stage 2: Entity Tuple Search
Our goal in the following stage is to search for entity tuples that achieves high compatibility with the weighted prompt set.
\[ \text{consistency} \left(\left\langle h^{\text {new }}, t^{\text {new }}\right\rangle\right)=\sum_p w_p \cdot f_{L M}\left(\left\langle h^{\text {new }}, t^{\text {new }}\right\rangle, p\right) \]
Since the entity search space is too large, we propose an approximation that only uses the minimum individual log-likelihoods (the left part of compatibility score, shortened as MLL) instead of the full equation. This cheaper scoring function allows fast rollouts by pruning.
As a running example, when we are searching for 100 entity tuples, we maintain a minimum heap to keep track of the MLL of the existing entity pair set. The maximum size of this heap is 100, and the heap top can be used as a threshold for future search because it’s the 100-th largest MLL: When we are searching for a new entity tuple, once we find the log-likelihood at any timestamp is lower than the threshold, we can prune the continuous searching immediately because this means the MLL of this tuple will never surpass any existing tuples in the heap. If a new entity tuple is reached without being pruned, we pop the heap and push the MLL of the new tuple.
Once we collect a large number of potential entity tuples, we re-rank them with the full compatibility score (as the confidence for them). We finally use various thresholds to get the outcome KGs in different scales, including (1) 50%: taking half of all searched-out entities with higher scores. (2) base-k: Naturally there are different numbers of valid tuples for different relations (e.g. tuples of CAPITAL_OF should not exceed 200 as that is the number of all the countries in the world). We design a relation-specific thresholding method, that is to set 10% of the k-nd score as the threshold (i.e., 0.1 ∗ score_k), and retain all tuples with scores above the threshold. We name the settings base-10 and base-100 when k is 10 and 100, respectively.
Outcome KGs
Different from traditional KGs, BertNet is extensible in case a new query is desired.. In essence, there is no limitation on the scalability of BertNet. In our evaluation, we ground our framework to a commonly used relation set from ConceptNet, and a New relation set composed of some novel relations created by the authors (e.g. “capable but not good at”).
\[ \begin{array}{lllcc} \hline \text { Method } & \text { Tuple } & \text { Diversity } & \text { Novelty\% } & \text { Acc\% } \\ \hline \text { WebChild } & 4,649,471 & - & - & 82.0^* \\ \text { ASCENT } & 8,600,000 & - & - & 79.2^* \\ \text { TransOMCS } & 18,481,607 & 100,659 & 98.3 & 56.0^* \\ \hline \text { COMET }_{\text {base-10 }}^{C N} & 6,741 & 4,342 & 35.5 & 92.0 \\ \text { COMET }_{50 \%}^{C N} & 230,028 & 55,350 & 72.4 & 66.6 \\ \hline \text { ROBERTANET }_{\text {base-10 }}^{C N} & 6,741 & 6,107 & 64.4 & 88.0 \\ \text { RoBERTANET }_{\text {base-100 }}^{C N} & 24,375 & 12,762 & 68.8 & 81.6 \\ \text { ROBERTANET }_{50 \%}^{C N} & 230,028 & 80,525 & 87.0 & 55.0 \\ \hline \text { RoBERTANET T }_{\text {base-10 }}^{\text {New }} & 2,180 & 3,137 & - & 81.8 \\ \text { RoBERTANET }_{\text {base-100 }}^{\text {New }} & 7,329 & 6,559 & - & 68.6 \\ \text { ROBERTANET }_{50 \%}^{\text {New }} & 23,666 & 16,089 & - & 58.6 \\ \hline \end{array} \] Table 1: Statistics of different knowledge graphs
Using solely the LM as the knowledge source, and without any training data, our framework extracts KGs with high accuracy and diversity. (Other methods in the table build knowledge graphs in different settings, and thus are not comparable to ours) We also show the trade-off between scale and accuracy by using different thresholds.
Summary
In this work, we propose an automatic framework for extracting a knowledge graph from language models with arbitrary relations in an efficient and scalable manner, and demonstrate its application in creating KGs of two sets of relations. Our results indicate that LMs can be effective resources for KG construction on their own. Our framework also offers a fully symbolic interpretation of the LM, providing new insights into its knowledge capabilities.